
지금까지 이런 사례는 없었다. 깡은 2017년 12월에 발매한 가수 비의 미니앨범 ‘마이 라이프(MY LIFE) 愛’의 타이틀곡이다. 당시 깡은 이른바 ‘실패한 노래’였다. 모든 음원 차트에서 ‘톱100’에 들지 못했고 음악적으로도 평론가들에게 혹평을 받았으며 음원, 뮤비 모두 반등하지 못한 채 빠르게 잊혔기 때문이다. 그런데 2020년에 갑자기 깡이 다시 실시간 차트에 진입했다. 뿐만 아니라 유튜브는 깡 챌린지로 범람하고 심지어 비는 깡으로 CF까지 찍었다. 묻혔던 좋은 노래가 입소문을 타며 다시 유행하는 일반적인 ‘역주행’과는 달리 깡의 역주행은 여전히 노래에 관한 평이 좋지 않다는 점에서 매우 이례적이다.
2020년 6월 5일 박재범, 김하온, pH-1, 식케이 등 요즘 가장 ‘핫’한 뮤지션들과 비가 만나 발매한 깡의 리믹스 버전인 ‘깡 오피셜 리믹스(Official Remix)’가 멜론, 지니, 벅스 등 주요 음원 차트 1위를 석권했다. 원곡도 멜론 차트 기준 18위까지 올랐다. 비는 리믹스 버전이 1위를 차지하자 소셜네트워크서비스(SNS)에 "이거 왜 이러는 거죠. 이상한데 깡동단결인가. 깡짝 놀랐네. 놀자고 한 일인데"라며 놀라움을 드러냈다.
혹평이 쌓여 열풍이 되다
개연성 없는 곡의 진행, 세련미 없이 자기애만 가득한 가사, 비의 매력을 잘 살리지 못한 안무 등 2017년 발매 당시 깡에 대한 대중의 평가는 저조했다. 실제 성적도 좋지 않았다. 그런데 그 악평이 인터넷에서 유행하는 소재를 일컫는 ‘밈’으로 떠올랐다. 깡의 문제점을 지적하는 웃긴 댓글들이 뮤직비디오에 연이어 달리면서 깡이 유명해진 것이다. 댓글을 보기 위해 깡을 찾는 사람이 점점 늘어나자 깡 뮤직비디오 댓글창은 ‘깡뮤니티’로 불리며 고정 유저층을 형성하기에 이르렀다.
아는 사람만 아는 놀이터였던 깡은 5월 1일 통계청이 남긴 댓글에 대한 논란이 기사화되면서 더욱 널리 알려졌다. 통계청 공식 유튜브 계정이 깡 뮤직비디오 댓글에 “통계청에서 깡조사 나왔습니다. 2020년 5월 1일 10:00 기준 비 RAIN- 깡 GANG Official 뮤직비디오 조회수 685만9592회 39.831UBD입니다”라고 남겼는데, ‘UBD’라는 단위는 비의 주연 영화인 ‘자전차왕 엄복동’의 저조한 관객 수 17만 명을 가리키는 인터넷 용어기 때문이다.
비의 입장에서 조롱이라 여겨질 수 있는 표현을 국가 기관에서 사용했다는 점이 논란이 됐고, 이후 통계청은 국민과 스스럼 없이 소통하고자 하는 과정에서 실수를 빚었다고 사과했다. 이 사건 이후 깡의 인지도는 더욱 높아졌고 비는 깡을 소재로 MBC 예능 ‘놀면 뭐하니?’에 출연해 토요일 비드라마 TV 화제성 1위를 기록했다.
갑작스러운 여론 변화
발매한 지 2년 반이나 지난 노래가 갑자기 큰 인기를 누리는 일은 흔치 않다. 깡의 경우 특정 방송에 나와서 유명해졌다거나 EXID ‘위아래’ 직캠처럼 뚜렷한 계기가 있는 것도 아니다. 통계청 논란이 대중에게 깡을 알리는 하나의 사건이 되기는 했지만 애초에 통계청이 댓글을 남긴 것도 깡이 어느 정도 유명했기 때문이므로, 깡 열풍의 직접적인 원인이라고 보기는 힘들다. 그토록 혹평에 시달리던 깡은 어떻게 여론을 뒤집고 대세로 자리한 걸까?
깡의 인기처럼 세상에는 결정적인 계기를 알 수 없는 급격한 변화가 많다. 방금 전까지 괜찮던 다리가 돌연 무너지기도 하고, 고요해 보이던 군중이 갑자기 폭동을 일으키며, 예측할 수 없는 상황에서 주가가 폭락한다. 이처럼 작은 변화에 의한 급격한 상태 전환을 설명하는 수학 이론이 ‘파국 이론’이다.
대변동을 설명하는 수학
파국 이론은 프랑스 수학자 르네 톰이 제안했다. 작은 변화가 쌓여 광범위한 큰 변동이 일어나는 현상을 수학적으로 분석하고 이해하는 방법이다. 수와 식뿐만 아니라 기하학적인 구조로 자연, 사회 현상을 설명한다.
파국 이론에서는 원인의 공간과 결과의 공간을 구분한다. 원인 공간에 있는 변수의 움직임에 따라 결과 공간에 있는 함숫값이 결정된다. 이때 결과 공간은 휘어진 곡면이므로 어떤 지점에서 급격한 변화가 일어나기도 하는데, 이러한 지점들을 ‘파국 지점’이라고 부른다. 파국 지점이 깡 인기에 어떻게 작용했는지 궁금하다면 아래 그림을 참고하자.
비는 예능 프로그램 ‘놀면 뭐하니?’에 출연해 깡을 둘러싼 대중의 반응에 직접 대응했다. 가수로서 충분히 기분이 나쁠 수 있을 만한 댓글에도 비는 “너무 재미있다. 더 놀아주셨으면 좋겠다.”며 대인배로서의 면모를 보였다. 비의 넓은 아량만큼 깡의 인기도 한동안 더욱 커질 것 같다.
● 파국이론으로 본 '깡'의 인기
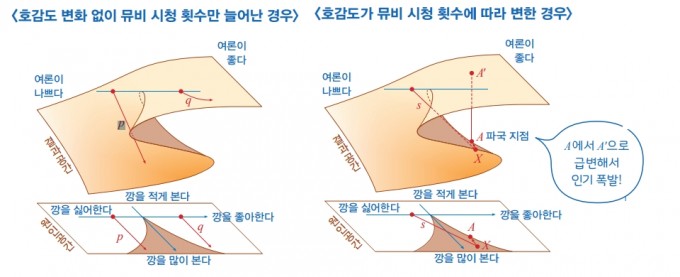
깡의 인기가 깡에 대한 호감도와 뮤비를 본 횟수의 영향을 받아 결정된다고 가정하자. 깡에 대한 호감도가 변하지 않 은 채 시청 횟수가 늘어날 때의 여론 변화는 위와 같다. 깡 을 싫어하는 사람이 깡 뮤비를 보는 것은 길 p를 따라 움 직이는 점으로 나타내낼 수 있고 결과 공간에서 곡면 위의 길 p는 점점 아래쪽으로 내려가 깡의 여론이 점차 나빠진 다. 반면 깡을 좋아하는 사람이 깡을 많이 보면 길 q를 따 라가고, 결과 공간에서 길 q는 점점 곡면 위쪽으로 올라가 므로 깡의 여론이 좋아질 거라고 예측할 수 있다.
처음 깡을 싫어했던 사람이 깡을 놀리기 위해 뮤비를 자주 시청했다고 하자. 자주 듣다 보니 조금씩 깡에 적응해 호감 도가 높아지기 시작한다. 그러면 곡면에서 그래프는 길 s를 따라 이동한다. 여전히 깡의 인기는 낮고 변화는 미미하다. 그런데 점 X 쯤에 이르러 깡에 대한 흥미가 줄어 깡 뮤비 를 보는 횟수가 조금 줄었다고 하자. 그러면 길 s는 점 X에 서 A 방향으로 꺾이는데, 결과 공간에서 점 A는 A′으로 급 변하는 파국 지점이다. 즉 이 위치를 지나면서 갑자기 깡의 여론에 급격한 변화가 일어나며 혹평 일색이었던 조롱 분 위기에서 국민적 인기를 누리는 대세로 떠오르게 된다.
※관련기사
수학동아 7월호 [주접평론가 피터팍의 아이돌 수학] 대한민국을 깡타한 '나 비 효과' 역주행의 신화 '깡'


